Date: 05-08-2025
A/B testing is one of the most commonly used methods for making product and marketing decisions. Traditionally, A/B testing relies on frequentist statistics, where we rely on p-values and predefined significance thresholds. However, the frequentist approach has limitations, especially when it comes to interpreting results in a real-world, data-driven context.
This is where Bayesian A/B testing comes into play — a more intuitive and robust approach to experimentation that provides clearer insights. In this post, we will:
- Build a Bayesian A/B testing app using Streamlit and PyMC.
- Compare Bayesian A/B testing with traditional hypothesis testing.
- Explain Type I and Type II errors.
- Clarify key statistical concepts such as null/alternative hypotheses, alpha, p-values, and more.
- Discuss the difference between one-tailed and two-tailed A/B testing.
What Is A/B Testing?
A/B testing (also known as split testing) is a controlled experiment where two groups (Group A and Group B) are exposed to different versions of a variable, and we compare the outcomes based on a metric (such as conversion rate or user retention).
For example, imagine a mobile game company wants to test whether changing the level gate in their game from level 30 to level 40 improves 1-day user retention. In this experiment:
- Group A (Control) sees the gate at level 30.
- Group B (Treatment) sees the gate at level 40.
After collecting data on user retention, we would compare the performance of both groups and decide which version (A or B) performs better.
Why Bayesian A/B Testing?
Traditional A/B testing methods ask the question, “Did something happen?” and rely on p-values to assess statistical significance. However, Bayesian A/B testing asks a more intuitive question:
“What’s the probability that B (treatment) is better than A (control)?”
Bayesian Inference Updates Belief
Bayesian testing involves updating our beliefs as new data becomes available using Bayes’ Theorem:
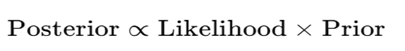
What does it mean:
When we are trying to update our beliefs after seeing new data, we use this formula in Bayesian statistics.
- Prior: Our belief about the parameters (e.g., probability of success for control and treatment) before seeing the data.
- Likelihood: The probability of observing the data given a certain hypothesis.
- Posterior: Our updated belief after observing the data.
Bayesian Approach: A More Intuitive Alternative
The main advantage of Bayesian methods is that they provide a posterior probability — the likelihood that one variation is better than the other. This allows us to directly answer:
“What’s the probability that the treatment outperforms the control, given the observed data?”
This approach offers several benefits:
- Intuitive probabilities: For example, a 92% chance that the treatment is better than the control.
- Full posterior distributions: We can see not just a point estimate, but the full uncertainty in the result.
- Incorporates prior knowledge: Bayesian methods allow you to integrate prior knowledge or historical data.
- Works well with smaller samples: Unlike traditional frequentist methods, Bayesian testing is more flexible in the presence of smaller sample sizes.
For example, after conducting a test, you might get an output like:
“There is an 89% probability that the treatment improves retention.”
This allows for data-driven decision-making with customizable thresholds (e.g., only implement changes if there’s a >90% chance of improvement).
Use Case: Cookie Cats Game Retention Test
In our case study, let’s explore the Cookie Cats game test. The game blocks players at level 30 unless they make a purchase or invite friends. The team is testing whether shifting the gate from level 30 to level 40 improves Day 1 retention. The hypotheses are as follows:
- Null Hypothesis (H₀): No effect (p_control = p_treatment).
- Alternative Hypothesis (H₁): There is a difference in retention between the control and treatment (p_control ≠ p_treatment).
Type I and II Errors
- Type I Error (False Positive): We mistakenly claim that moving the gate improves retention when it actually doesn’t.
- Type II Error (False Negative): We mistakenly claim that moving the gate has no effect when it actually does.
These errors are critical when designing A/B tests, and understanding how to minimize them is key to obtaining valid results.
Classical vs Bayesian A/B Testing
| Aspect | Classical A/B Testing | Bayesian A/B Testing |
| Output | p-value | Posterior probability |
| Decision Rule | p < α (usually 0.05) | P(treatment > control) > threshold |
| Prior Knowledge | Not used | Explicitly used |
| Interpretation | Indirect (reject or fail to reject) | Direct (probability) |
Bayesian Modeling with PyMC
Here’s how to implement a simple Bayesian A/B test using PyMC:

This code sets Beta(1,1) priors (uniform belief) and uses observed retention data from both control and treatment groups to update our beliefs.
- α (alpha): the number of successes (e.g., users who retained)
- β (beta): the number of failures (e.g., users who did not retain)
Posterior Interpretation
After sampling, we can interpret the posterior distribution:

Interpretation: “There’s a 92% probability that moving the gate to level 40 increases retention.”
Streamlit App for A/B Testing
To visualize our Bayesian analysis, let’s build an interactive Streamlit app:

This app allows users to upload their own data and visualize the results of the Bayesian analysis in real-time.
🔹 Final Thoughts
- A/B testing is essential for understanding product changes.
- Bayesian A/B testing provides more intuitive results and offers a better understanding of the probability that one version is better than the other.
- With Bayesian A/B testing, you gain access to full uncertainty distributions, helping you make more informed decisions.
- This method is especially valuable when dealing with smaller sample sizes or when you have strong prior knowledge about the problem.
For critical product decisions, Bayesian testing provides a deeper, more meaningful insight than traditional p-value-based methods.
